Problems - page 3
Given a triangle $ABC$ with its incircle $\omega$ touching $BC$, $CA$, and $AB$ at $D$, $E$, and $F$ respectively. Let $P$ be the external homothety center of $\omega$ and $(ABC)$. Suppose the rays opposite to $PB$ and $PC$ intersect $\omega$ at $Q$ and $R$. Let $M$ and $N$ be the reflections of $D$ across $Q$ and $R$, respectively. Choose $J$ such that $JM \parallel EQ$ and $JN \parallel FR$. On the sides $DE$ and $DF$, select points $K$ and $L$ such that $EL = ED$ and $FK = FD$. Prove that the circles $(DKL)$ and $(JMN)$ are tangent to each other.

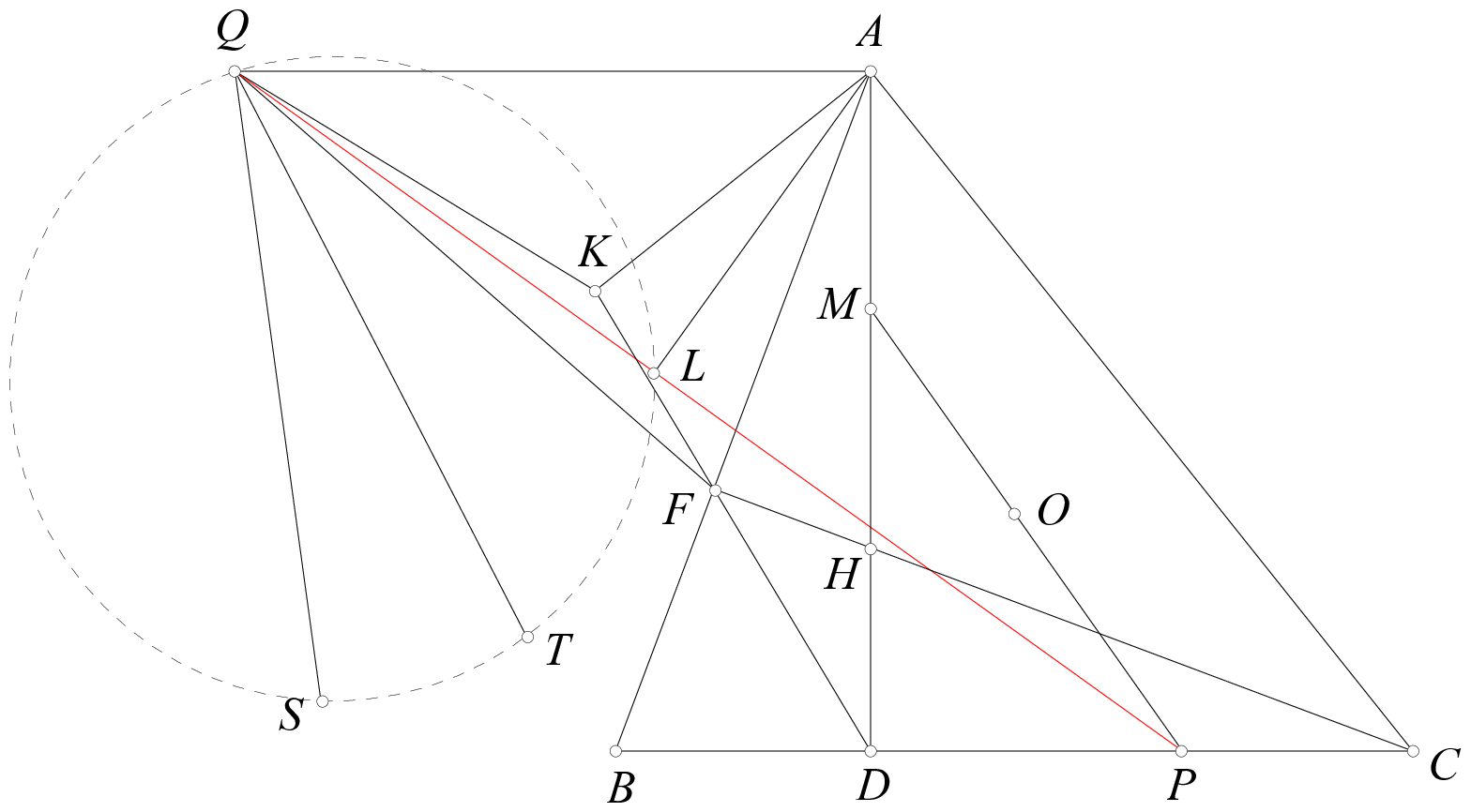
Let $ABC$ be a triangle inscribed in the circle $(O)$, with the altitudes $AD$ and $CF$ intersecting at the orthocenter $H$. Let $M$ be the midpoint of $AH$. The line $OM$ intersects $BC$ at $P$. Let $Q$ be a point such that $AQ \parallel BC$ and $MQ \perp AB$. Point $K$ lies on $DF$ such that $AK \perp AC$. Points $S$ and $T$ are the reflections of $A$ over the lines $QK$ and $QF$, respectively. Let $L$ be the projection of $A$ onto $PQ$. Prove that $Q, L, S, T$ are concyclic.