Problems - page 2
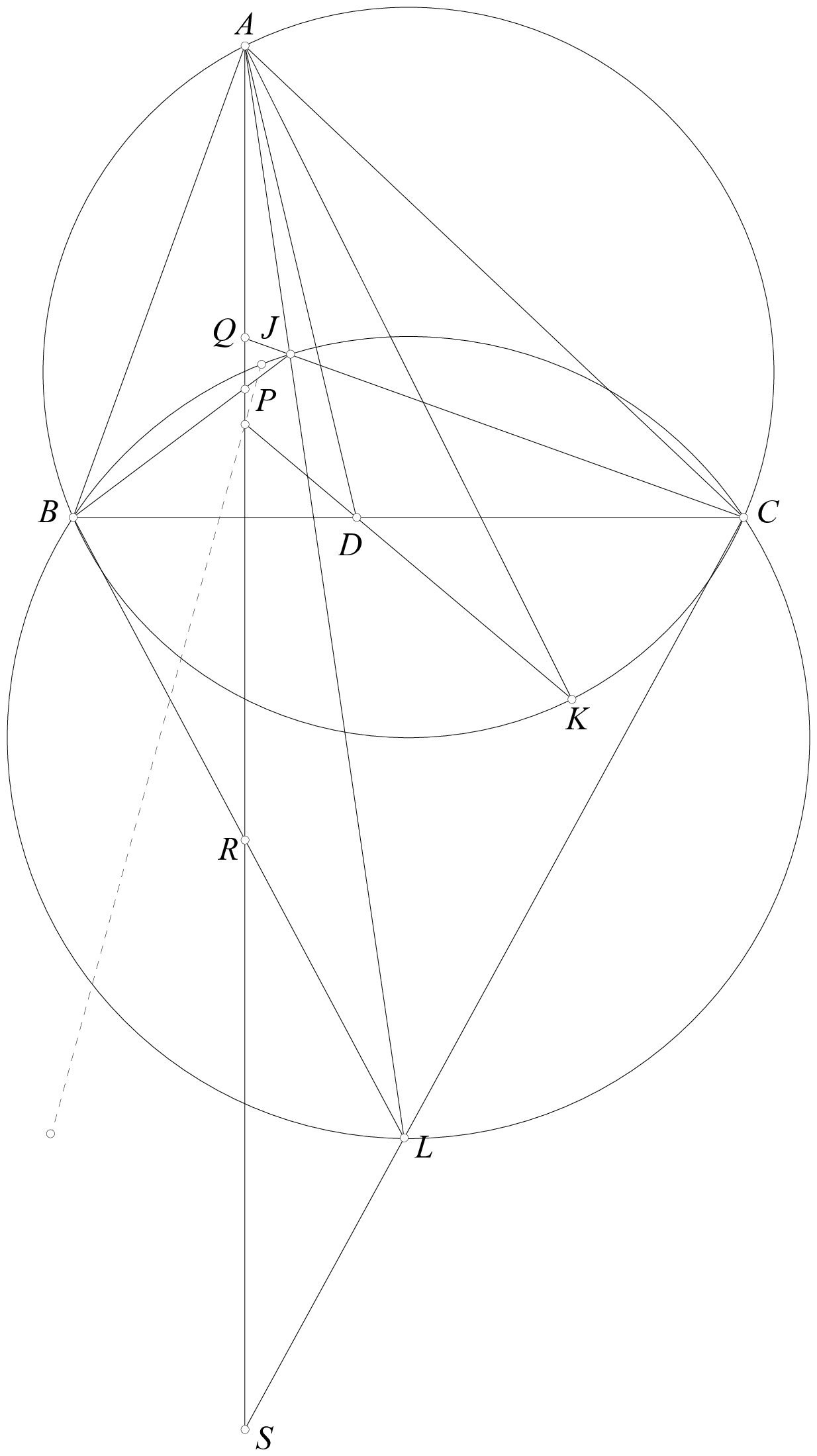
Given a triangle $ABC$ with the Kosnita point $K$. Let $AK$ intersect the circle $(KBC)$ again at $L$. On the tangent line through $A$ to the circumcircle $(ABC)$, take a point $S$ such that $SA = SL$. Prove that the line $BC$ bisects $AS$.
Given a triangle $ABC$ inscribed in a circle $(O)$. Let $D$ be a point on $(O)$ such that the line $AD$ intersects $(BOC)$ at points $E$ and $F$. Let $P$ be an arbitrary point on $(BOC)$. The lines $PE$ and $PF$ intersect $BC$ at points $M$ and $N$, respectively. The circle $(PMN)$ intersects $(O)$ at points $Q$ and $R$. Prove that if $AQ$ and $RD$ are concurrent with $BC$, then $DQ$ and $AR$ intersect on $(PQR)$, or vice versa.
Prove that the convex hexagon $ABCDEF$ will have parallel opposite sides if \((AB+DE)^2+(BC+EF)^2+(CD+FA)^2=AD^2+BE^2+CF^2.\)
LinkLet $ABC$ be a triangle with $L$ as the reflection of the orthocenter over the circumcenter. Let $D, E, F$ be the projections of $L$ onto $BC, CA, AB$ respectively. Prove that $AD, BE, CF$ are concurrent at a point lying on the line connecting the circumcenter of triangle $ABC$ and the symmedian point of triangle $DEF$.
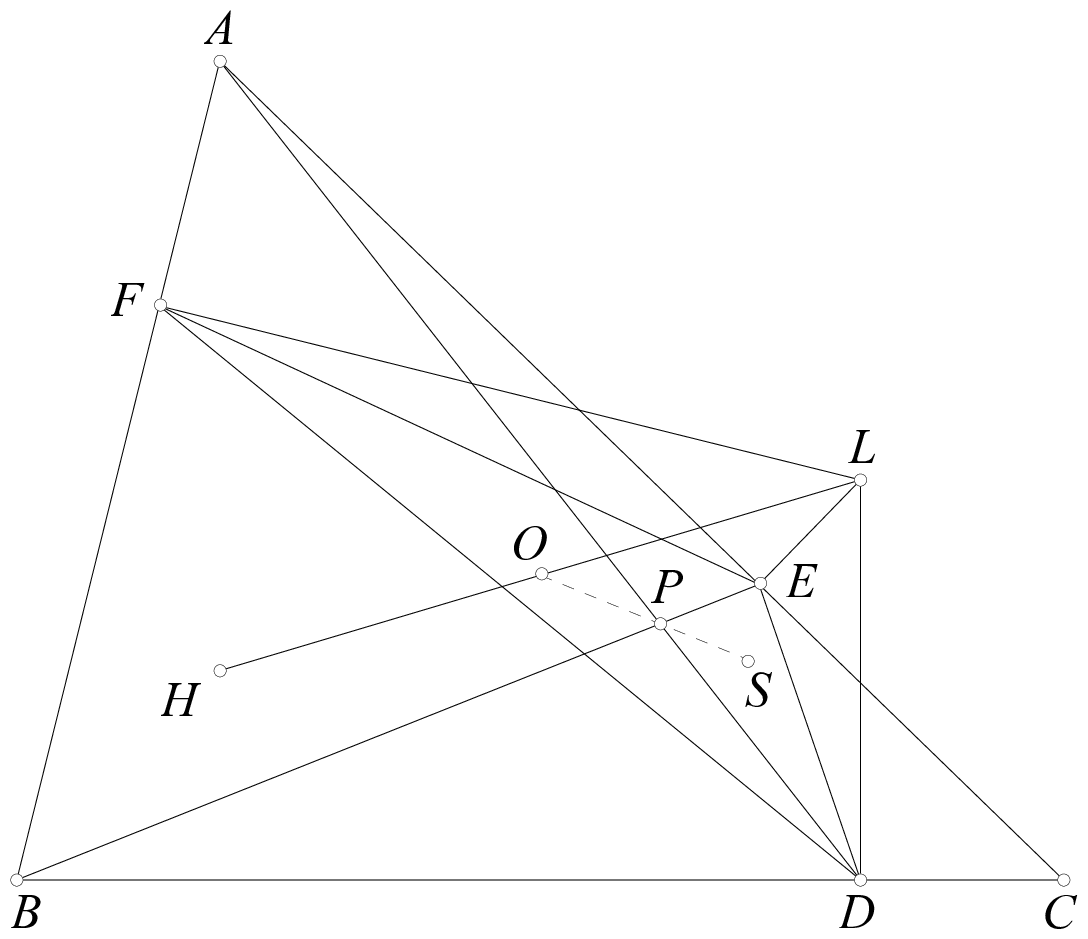
Given a triangle $ABC$. A circle $\Gamma$ is tangent to $(ABC)$ at $A$ and tangent to side $BC$ at $D$. The circle $\Gamma$ intersects $CA$ and $AB$ at $E$ and $F$, respectively. Let $K$ and $L$ be the reflections of $D$ across $C$ and $B$, respectively. Let $P$ be the intersection of lines $LF$ and $KE$. The lines $PF$ and $PE$ intersect $\Gamma$ again at $M$ and $N$, respectively. Let $DJ$ be the diameter of $\Gamma$. The perpendicular bisector of $KL$ intersects line $AD$ at $X$. Prove that the circles $(PMN)$, $(XKL)$, and $(J, JD)$ are tangent to each other.
Given a triangle $ABC$, let $D$ be the point where the incircle $(I)$ touches $BC$. The line through $I$ parallel to $BC$ intersects $CA$ and $AB$ at points $E$ and $F$, respectively. Let $J$ and $L$ be the reflections of $I$ over $DF$ and $DE$, respectively. Point $P$ is chosen inside triangle $ABC$ such that $DP \parallel AI$ and $DP \cdot AI = ID^2$. The line $PI$ intersects the perpendicular bisector of $JL$ at $K$. Prove that the circle $(K)$, passing through $J$ and $L$, is tangent to the circle centered at $A$ that passes through $I$.
Given a triangle $ABC$ with its incircle $\omega$ touching $BC$, $CA$, and $AB$ at $D$, $E$, and $F$ respectively. Let $P$ be the external homothety center of $\omega$ and $(ABC)$. Suppose the rays opposite to $PB$ and $PC$ intersect $\omega$ at $Q$ and $R$. Let $M$ and $N$ be the reflections of $D$ across $Q$ and $R$, respectively. Choose $J$ such that $JM \parallel EQ$ and $JN \parallel FR$. On the sides $DE$ and $DF$, select points $K$ and $L$ such that $EL = ED$ and $FK = FD$. Prove that the circles $(DKL)$ and $(JMN)$ are tangent to each other.
